尾部风险是投资组合风险的一种形式，当一项投资偏离均值超过三个标准差的可能性大于正态分布所显示的值时，就会出现这种风险。
尾部风险包括发生概率较小且发生在正态分布曲线两端的事件。
关键要点
- 尾部风险是由概率分布预测的由于罕见事件而发生损失的可能性。
- 通俗地说，超过三个标准差的短期移动被认为是尾部风险的实例化。
- 虽然尾部风险在技术上指的是左右尾，但人们最关心的是损失（左尾）。
- 尾部事件让专家质疑可投资资产回报的真实概率分布。
了解尾部风险
传统的投资组合策略通常遵循市场回报服从正态分布的想法。然而，尾部风险的概念表明，收益的分布不是正态的，而是偏斜的，并且有更肥的尾巴。
肥尾表明，投资有可能超过三个标准差 ，这可能比预期的要大。例如，在查看对冲基金回报 时，经常会看到以肥尾为特征的分布。
下图描绘了三个向右偏斜增加的曲线，肥尾向下，与正态分布 的对称钟形曲线形状不同。
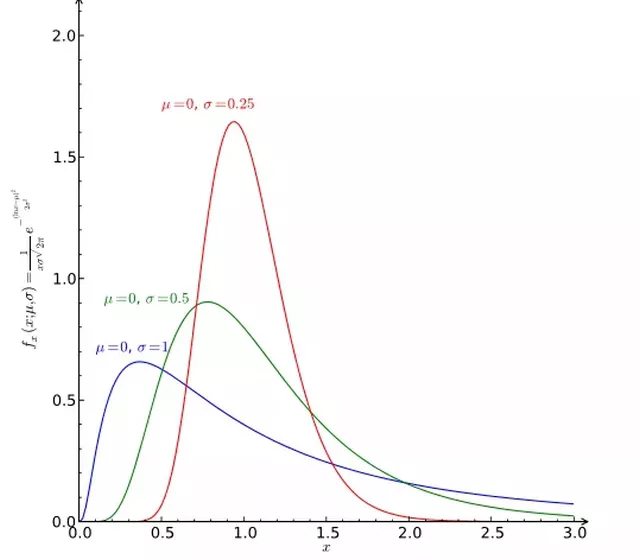右偏度。正态分布和资产回报
当投资组合放在一起时，假设收益分布将遵循正态分布。在此假设下，收益在均值和三个标准差（正或负）之间变动的概率约为 99.7%。这意味着收益超出均值超过三个标准差的概率为 0.3%。
市场收益服从正态分布的假设是许多金融模型的关键，例如 Harry Markowitz 的现代投资组合理论 (MPT)和 Black-Scholes-Merton期权定价模型。然而，这种假设并不能正确反映市场收益，尾部事件对市场收益的影响很大。
Nassim Taleb 的畅销金融书籍《黑天鹅》中强调了尾部风险。
其他分布及其尾巴
股票市场回报倾向于遵循具有过度峰度的正态分布。峰度是一种统计量度，表明观察到的数据是否遵循与正态分布相关的重尾分布或轻尾分布。正态分布曲线的峰度等于 3，因此，如果证券遵循峰度大于 3 的分布，则称其为肥尾。
尖峰分布，或重/肥 尾分布，描述了极端结果发生得比预期多的情况。与正态分布相比，这些曲线具有过多的峰度。因此，遵循这种分布的证券所经历的回报超过了平均值的三个标准差，超过了观察结果的 0.3%。
下图描绘了正态分布（绿色）以及越来越多的尖峰曲线（红色和蓝色），它们显示出肥尾。
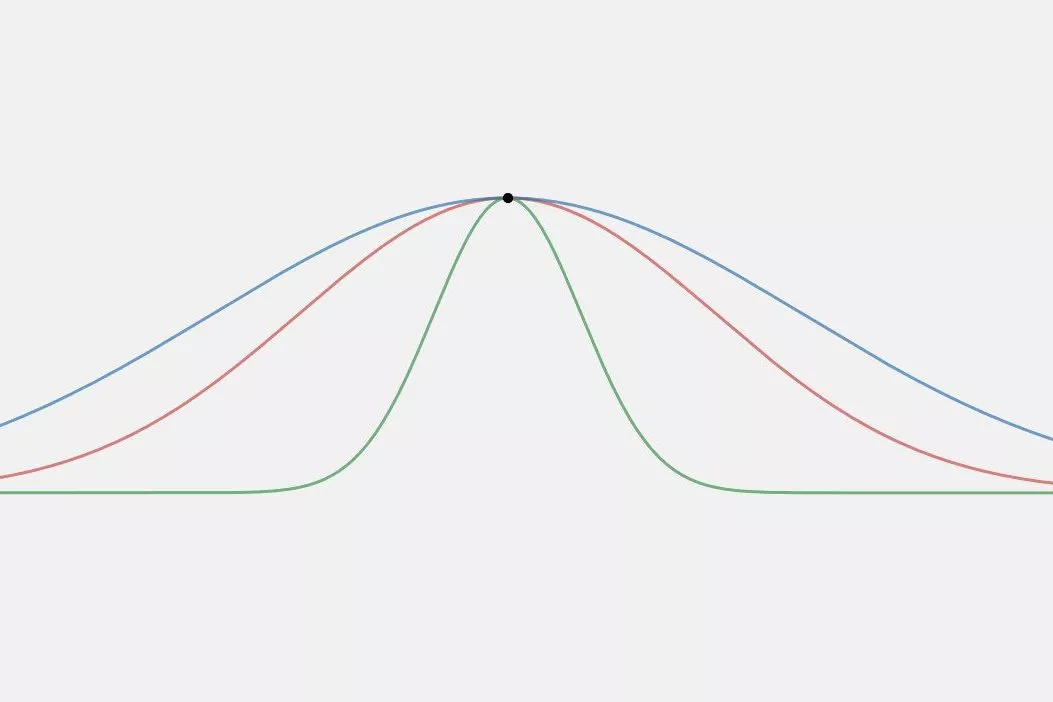峰度描述了概率分布可能具有的不同类型的峰值。
思想公司
对冲尾部风险
尽管对投资组合产生负面影响的尾部事件很少见，但它们可能会产生很大的负回报。因此，投资者应对冲这些事件。对冲尾部风险旨在提高长期回报，但投资者必须承担短期成本。投资者可能希望分散他们的投资组合以对冲尾部风险。
例如，如果投资者是跟踪标准普尔 500 指数 (S&P 500) 的多头交易所交易基金 (ETF) ，则投资者可以通过购买与 Cboe 波动率指数成反比的衍生品来对冲尾部风险。标准普尔 500 指数。
