AI 智能摘要
資本資產定價模型 (CAPM) 描述了系統性風險或投資的一般風險與資產(尤其是股票)的預期回報之間的關係。1CAPM 演變為一種衡量這種系統性風險的方法。考慮到這些資產的風險和資本成本,它在整個金融領域被廣泛用於對風險證券進行定價並為資產產生預期回報。
資本資產定價模型 – CAPM
了解資本資產定價模型 (CAPM)
給定風險的資產的預期收益計算公式如下:1
\begin{aligned} &ER_i = R_f + \beta_i (ER_m – R_f) \\ &\textbf{其中:} \\ &ER_i = \text{預期投資回報} \\ &R_f = \text{無風險利率} \ \ &\beta_i = \text{投資的beta} \\ &(ER_m – R_f) = \text{市場風險溢價} \\ \end{對齊}ER _一世=RF+b一世( E R米−RF)在哪裡:ER _一世=預期投資回報RF=無風險利率b一世=投資的貝塔( E R米−RF)=市場風險溢價
投資者期望得到補償的風險和貨幣的時間價值。CAPM 公式中的無風險利率說明了貨幣的時間價值。CAPM 公式的其他組成部分說明了投資者承擔的額外風險。
潛在投資的貝塔是衡量該投資會給看起來像市場的投資組合增加多少風險的指標。如果一隻股票比市場風險更大,它的貝塔係數就會大於 1。如果一隻股票的貝塔係數小於 1,則該公式假定它將降低投資組合的風險。
然後將股票的貝塔乘以市場風險溢價,即市場預期的高於無風險利率的回報。然後將無風險利率加到股票的貝塔和市場風險溢價的乘積上。結果應該為投資者提供他們可以用來找到資產價值 的所需回報或貼現率。
CAPM 公式的目標是評估當股票的風險和貨幣時間價值與其預期收益進行比較時,它的估值是否公允。換句話說,通過了解 CAPM 的各個部分,可以判斷股票的當前價格是否與其可能的回報一致。
例如,假設一位投資者正在考慮今天每股價值 100 美元的股票,該股票每年支付 3% 的股息。與市場相比,該股票的貝塔係數為 1.3,這意味著它比市場投資組合風險更大。此外,假設無風險利率為 3%,該投資者預計市場價值每年上漲 8%。
基於 CAPM 公式的股票預期回報率為 9.5%:
\begin{aligned} &9.5\% = 3\% + 1.3 \times ( 8\% – 3\% ) \\ \end{aligned}9.5%=3%+1.3×(8%−3%)
CAPM 公式的預期收益用於折現股票在預期持有期間的預期股息和資本增值。如果這些未來現金流的貼現值等於 100 美元,那麼 CAPM 公式表明股票相對於風險的估值是公允的。
CAPM 的問題
CAPM 公式背後的幾個假設已被證明在現實中不成立。現代金融理論基於兩個假設:第一,證券市場非常有競爭力和效率(即,有關公司的相關信息可以迅速、普遍地分布和吸收);第二,這些市場由理性的、規避風險的投資者主導,他們尋求最大程度地滿足他們的投資回報。
因此,CAPM 是否有效尚不完全清楚。最大的癥結在於測試版。當 Eugene Fama 和 Kenneth French 教授研究紐約證券交易所、美國證券交易所和納斯達克的股票回報時,他們發現長期貝塔的差異並不能解釋不同股票的表現。貝塔係數和個股回報率之間的線性關係也會在較短的時間內分解。這些發現似乎表明 CAPM 可能是錯誤的。2
儘管存在這些問題,但 CAPM 公式仍然被廣泛使用,因為它簡單並且可以輕鬆比較投資選擇。
在公式中包含貝塔假設風險可以通過股票的價格波動來衡量。然而,兩個方向的價格變動風險並不相同。確定股票波動率的回溯期不是標準的,因為股票收益(和風險)不是正態分布的。
CAPM 還假設無風險利率在貼現期內保持不變。假設在前面的例子中,美國國債的利率在 10 年的持有期內上升到 5% 或 6%。無風險利率的提高也會增加投資所用資金的成本,並可能使股票看起來被高估。
用於尋找市場風險溢價的市場組合只是一個理論值,而不是可以作為股票的替代品購買或投資的資產。大多數時候,投資者會使用標準普爾500等主要股票指數來替代市場,這是一個不完美的比較。
對 CAPM 最嚴重的批評是假設可以為貼現過程估計未來現金流量。如果投資者可以高度準確地估計股票的未來回報,則不需要 CAPM。
CAPM 和有效前沿
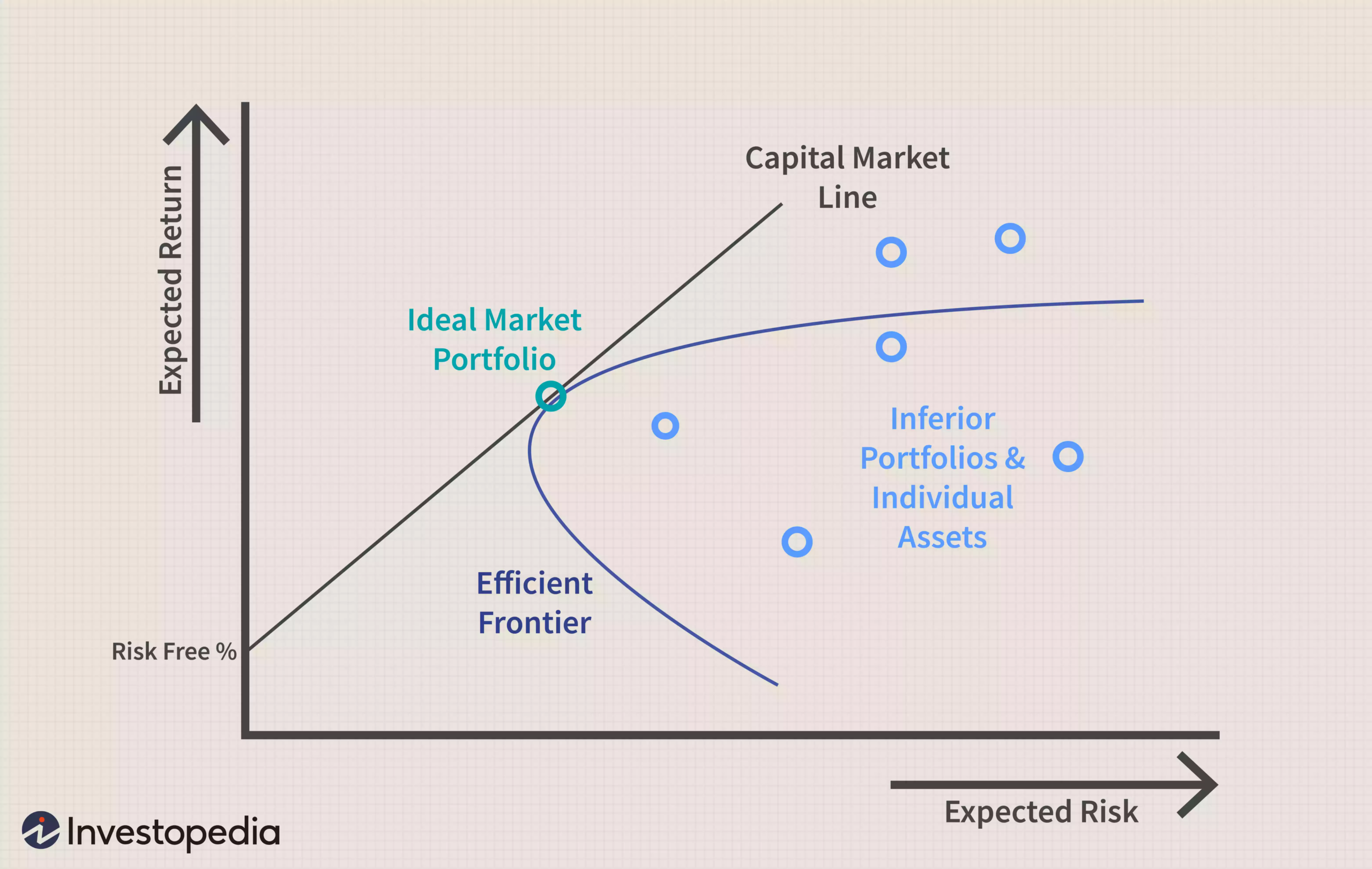
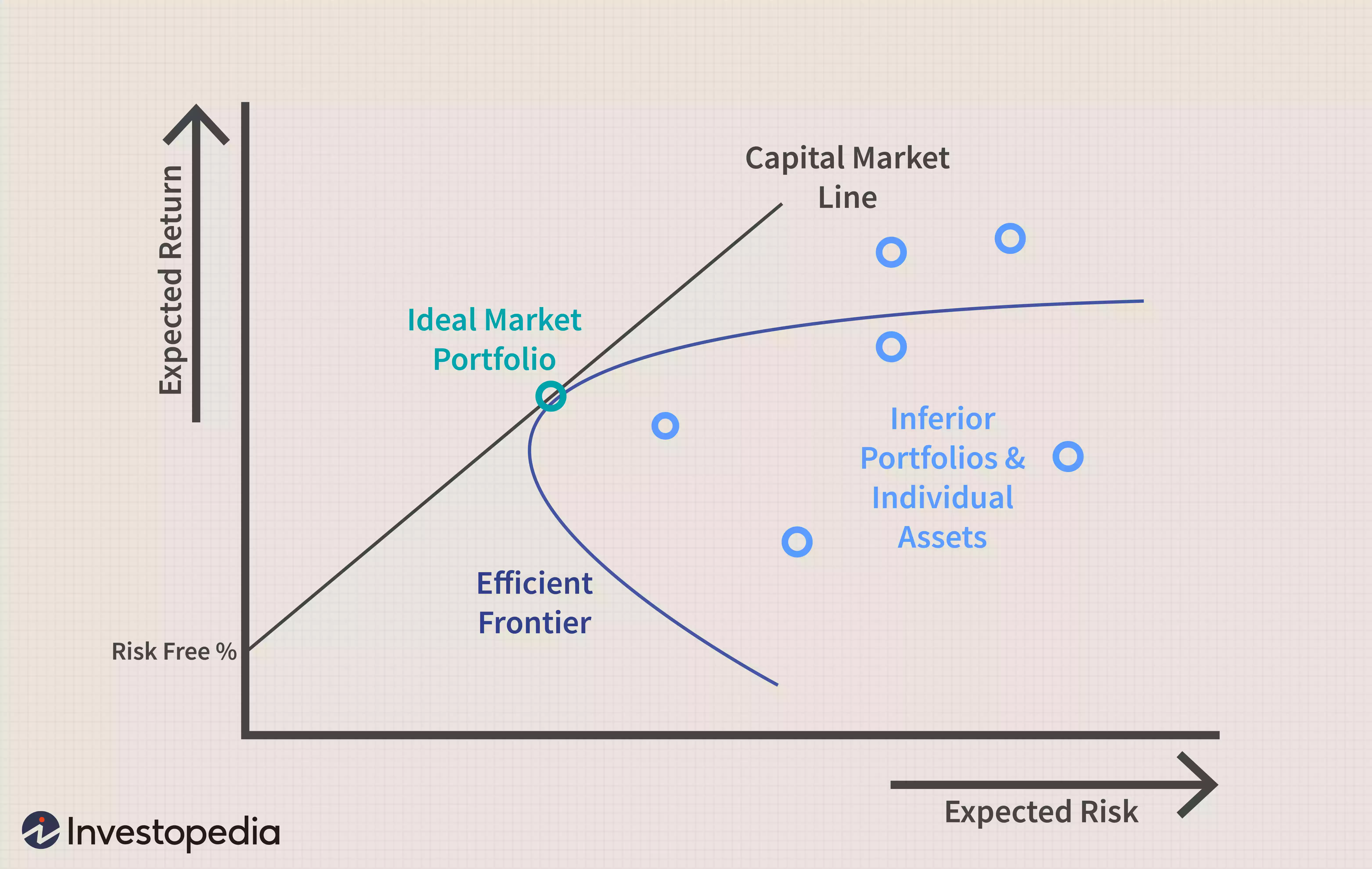
使用 CAPM 建立投資組合應該可以幫助投資者管理風險。如果投資者能夠使用 CAPM 來完美優化投資組合相對於風險的回報,它將存在於一條稱為有效前沿的曲線上,如下圖所示。
圖片由 Julie Bang © Investopedia 2022
該圖顯示了更大的預期回報(y 軸)如何需要更大的預期風險(x 軸)。現代投資組合理論 (MPT)表明,從無風險利率開始,投資組合的預期收益隨著風險的增加而增加。任何適合資本市場線 (CML)的投資組合都比該線右側的任何可能的投資組合要好,但在某些時候,可以在 CML 上構建理論投資組合,並在所承擔的風險量下獲得最佳回報.
CML 和有效邊界可能難以定義,但它們向投資者說明了一個重要概念:增加回報和增加風險之間存在權衡。由於不可能完美地構建適合 CML 的投資組合,因此投資者在尋求額外回報時承擔過多風險更為常見。
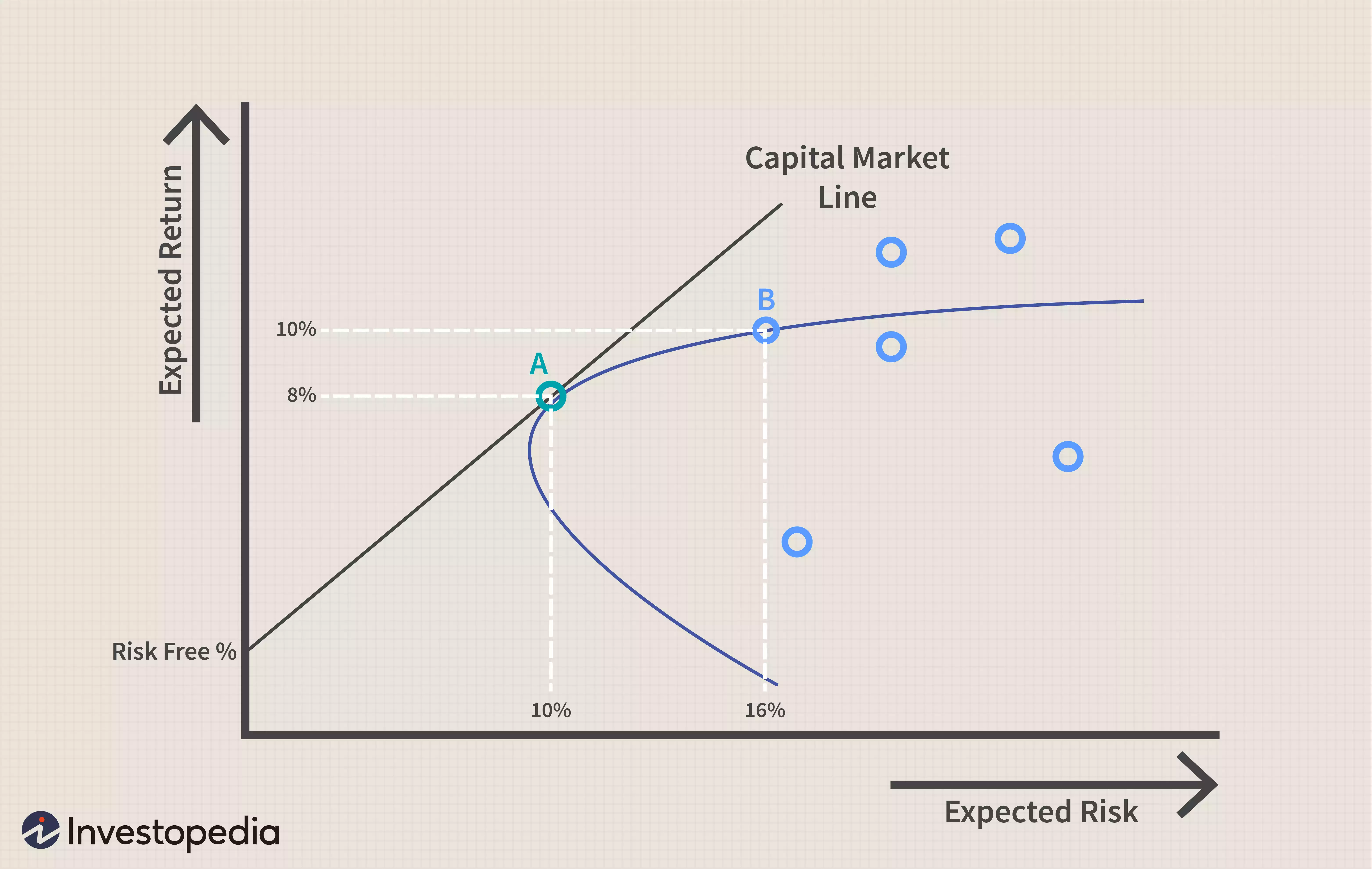
在下圖中,您可以看到兩個已構建以適應有效邊界的投資組合。投資組合 A 預計每年的回報率為 8%,標準差或風險水平為 10%。投資組合 B 預計每年的回報率為 10%,但標準差為 16%。投資組合 B 的風險上升速度快於預期回報。
圖片由 Julie Bang © Investopedia 2022
有效邊界假設與 CAPM 相同,只能在理論上計算。如果投資組合存在於有效邊界上,它將為其風險水平提供最大回報。但是,不可能知道投資組合是否存在於有效前沿,因為無法預測未來收益。
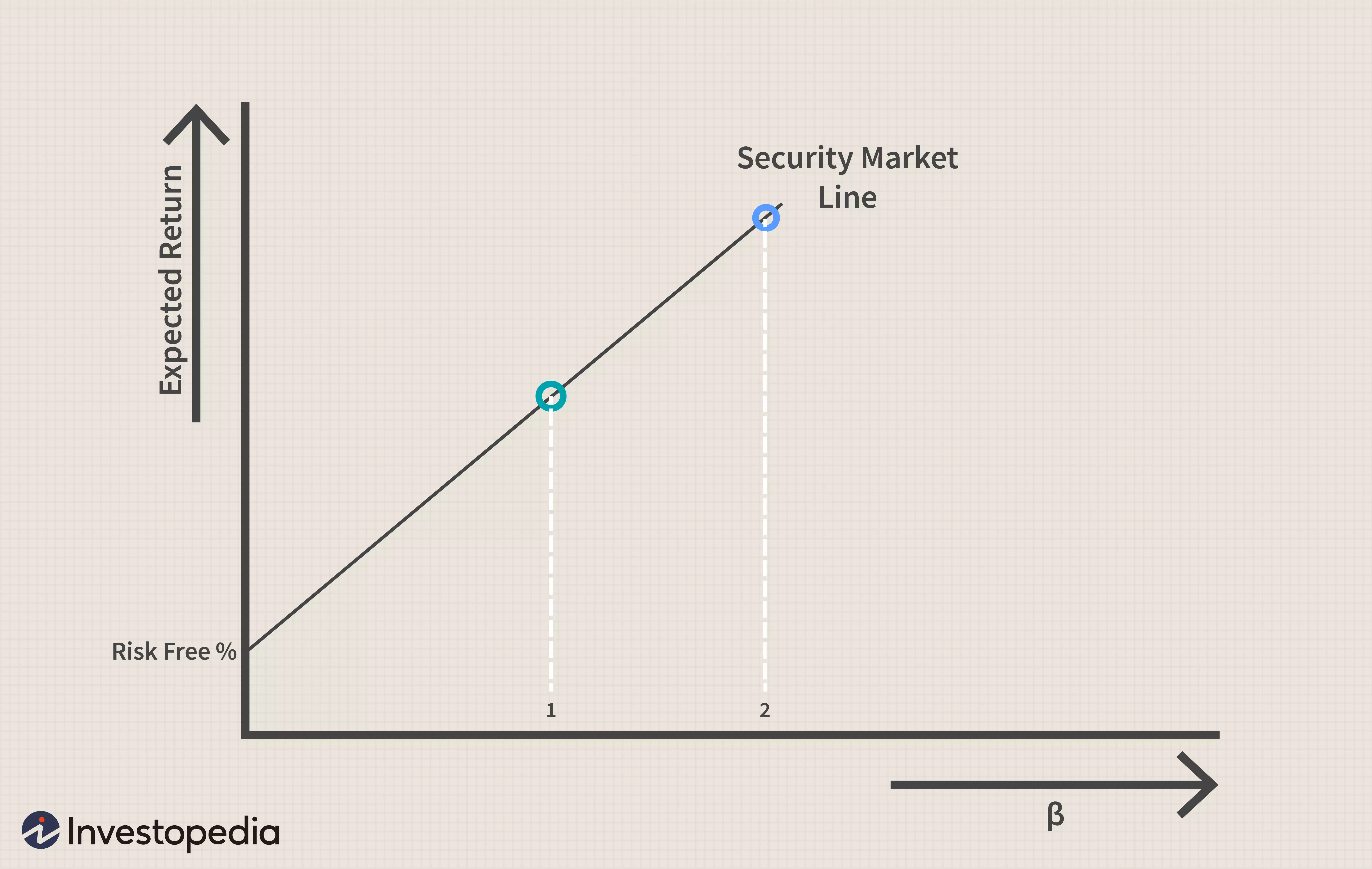
這種風險和回報之間的權衡適用於 CAPM,並且可以重新排列有效邊界圖以說明單個資產的權衡。在下圖中,您可以看到 CML 現在稱為證券市場線 (SML)。而不是 x 軸上的預期風險,而是使用股票的貝塔值。正如您在插圖中看到的,隨著 beta 從 1 增加到 2,預期回報也在上升。
圖片由 Julie Bang © Investopedia 2022
CAPM 和 SML 將股票的貝塔係數與其預期風險聯繫起來。Beta 是通過對單個每日股價回報與市場在同一時期的每日回報進行比較的統計分析得出的。更高的貝塔意味著更多的風險,但高貝塔股票組合可能存在於 CML 上的某個地方,即使不是理論上的理想,也可以接受權衡。
這兩個模型的價值被關於貝塔和市場參與者的假設削弱了,這些假設在真實市場中是不真實的。例如,與另一隻具有相同高貝塔但沒有經歷相同類型的價格下跌的股票相比,貝塔值並不能說明比市場波動更大、下行衝擊頻率高的股票的相對風險。 .
CAPM的實用價值
考慮到對 CAPM 的批評以及其在投資組合構建中使用背後的假設,可能很難看出它有什麼用處。但是,使用 CAPM 作為評估未來預期合理性或進行比較的工具仍然具有一定的價值。
想像一下,一位顧問建議以 100 美元的股價將一隻股票添加到投資組合中。顧問使用 CAPM 以 13% 的折扣率證明價格合理。顧問的投資經理可以獲取這些信息並將其與公司過去的業績和同行進行比較,看看 13% 的回報是否是一個合理的預期。
假設在這個例子中,同行集團在過去幾年的表現略好於 10%,而這隻股票一直表現不佳,回報率為 9%。投資經理不應在沒有為增加的預期回報提供理由的情況下接受顧問的建議。
投資者還可以使用 CAPM 和有效前沿的概念來評估他們的投資組合或個股與市場其他部分的表現。例如,假設投資者的投資組合在過去三年中每年的回報率為 10%,回報率(風險)的標準差為 10%。然而,過去三年市場平均回報率為 10%,風險為 8%。
投資者可以利用這一觀察結果重新評估他們的投資組合是如何構建的,以及哪些資產可能不在 SML 上。這可以解釋為什麼投資者的投資組合在 CML 的右側。如果可以識別出拖累回報或不成比例地增加投資組合風險的持股,投資者可以做出改變以提高回報。毫不奇怪,CAPM 促進了規避風險的投資者使用指數或組合股票組合以模仿特定市場或資產類別的增加。這主要是由於 CAPM 的信息,即只有通過承擔更高的風險(beta)才能獲得比整個市場更高的回報。
底線
CAPM 使用現代投資組合理論的原則來確定證券是否被公允估值。它依賴於與現實不符的投資者行為、風險和回報分布以及市場基本面的假設。然而,CAPM 的基本概念和相關的有效邊界可以幫助投資者理解預期風險和回報之間的關係,因為他們努力做出關於將證券添加到投資組合的更好決策。