波动率面是一个三维图，显示了在其上列出的股票期权在不同执行价格和到期日 的隐含波动率。
并非同一股票的所有期权都具有相同的隐含波动率 (IV)。这些差异的存在是由于市场对具有不同特征的股票期权的定价方式以及股票期权定价模型所说的正确价格应该是多少的差异。
为了更全面地了解这种现象，了解股票期权、股票期权定价和波动率表面的基础知识非常重要。
关键要点
- 波动率表面是指在同一股票上列出的各种期权的隐含波动率的三维图。
- 隐含波动率用于期权定价，以显示期权标的股票在期权有效期内的预期波动率。
- Black-Scholes 模型是一种著名的期权定价模型，它在期权定价公式中使用波动率作为其变量之一。
- 波动率表面随时间变化并且远非平坦，这表明 Black-Scholes 模型的假设并不总是正确的。
股票期权基础
股票期权是一种特定类型的衍生证券，赋予所有者执行交易的权利，但没有义务。在这里，我们讨论一些基本类型的股票期权。
看涨期权
看涨期权赋予所有者在特定日期（称为到期日）或之前以特定预定价格（称为行使价（或行使价））购买期权 标的股票的权利。当标的股票价格上涨时，看涨期权的所有者获利。
看跌期权
看跌期权赋予所有者 在特定日期或之前以特定价格出售期权标的股票的权利。当标的股票价格下跌时，看跌期权的所有者获利。
其他期权类型
此外，虽然这些名称与地理无关，但欧式期权只能在到期日执行。相反，美式期权可以在到期日或之前执行。其他类型的期权结构也存在，例如百慕大期权。
期权定价基础
Black-Scholes 模型是由 Fisher Black、Robert Merton 和 Myron Scholes 在 1973 年开发 的一种期权定价模型，用于对期权定价。1该模型需要六个假设才能起作用：
- 标的股票不支付股息，也永远不会。
- 该选项必须是欧式的。
- 金融市场是有效的。
- 交易不收取任何佣金。
- 利率保持不变。
- 标的股票收益呈对数正态分布。2
为期权定价的公式稍微复杂一些。它使用以下变量：当前股票价格、距离期权到期的时间、期权的执行价格、无风险利率、股票收益的标准差或波动率。在这些变量之上，该公式使用累积标准正态分布和数学常数“e”，大约为 2.7183。
波动率表面
在 Black-Scholes 模型中使用的所有变量中，唯一不确定的是波动性。在定价时，所有其他变量都是清楚且已知的，但波动性必须是估计值。波动率面是一个三维图，其中 x 轴是到期时间，z 轴是执行价格，y 轴是隐含波动率。如果 Black-Scholes 模型完全正确，那么执行价格和到期时间的隐含波动率表面应该是平坦的。在实践中，情况并非如此。
由于 Black-Scholes 模型的假设并不总是正确的，因此波动率表面远非平坦，并且经常随时间变化。例如，行使价较低的期权往往比行使价较高的期权具有更高的隐含波动率。
随着到期时间接近无限，执行价格的波动趋于收敛到一个恒定水平。然而，经常观察到波动率表面具有反向波动率微笑。与到期日较长的期权相比，到期时间较短的期权的波动性是其数倍。这种观察在市场压力较大的时期更为明显。应该注意的是，每条期权链都是不同的，波动率表面的形状可能会随着执行价格和时间而波动。此外，看跌期权和看涨期权通常具有不同的波动率表面。
当您从平价行权价上调或下调行权价时，隐含波动率可能会随着时间的推移而增加或减少，从而产生一种称为波动率微笑的形状，因为它看起来像一个人在微笑。
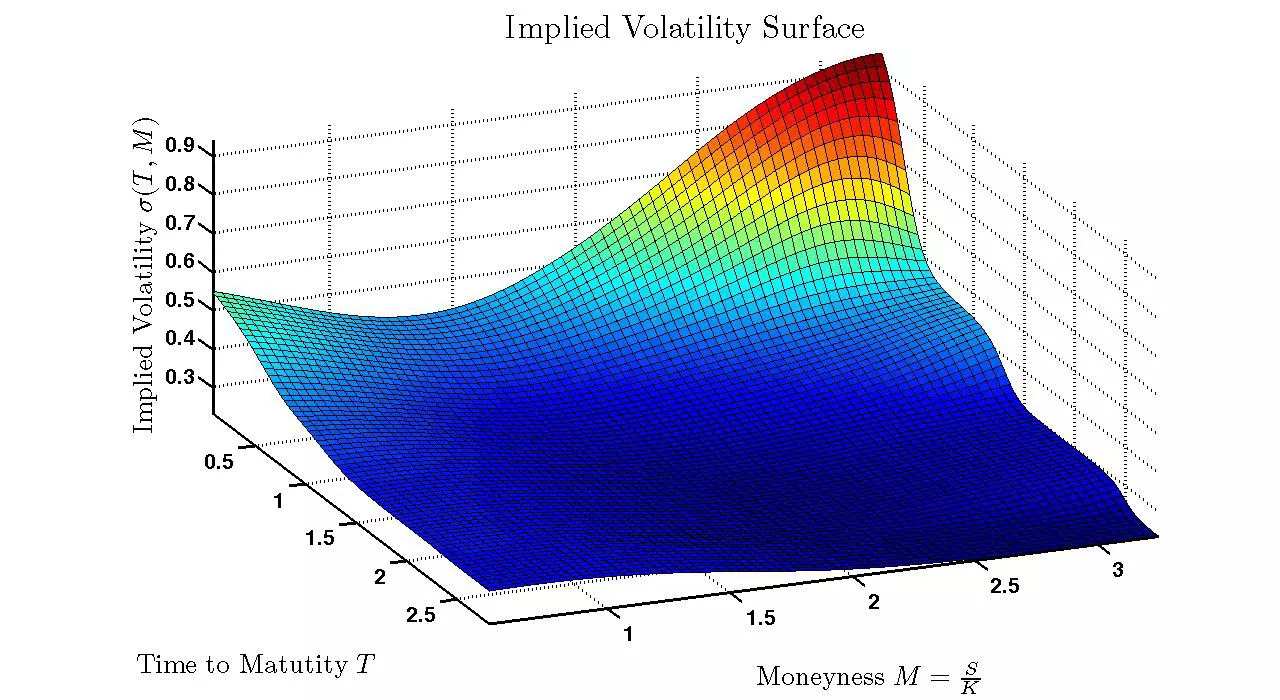波动率表面示例。为什么会存在波动率偏斜？
自 1980 年代后期以来，期权交易者已经认识到，下行看跌期权在市场中的隐含波动率比他们的模型预测的要高。这是因为天生多头的投资者和交易者会出于保险目的购买保护性看跌期权。这抬高了看跌期权相对于上行期权的价格。因此，往往存在波动率偏斜。如果上行期权也被买入，有时是由于对潜在收购的预期，那么就会出现波动率微笑，因为这两个极端都增加了隐含波动率。
什么是局部波动率？
局部波动率仅考虑整体波动率表面的一小部分的隐含波动率。它可能只关注一个期权，无论是看涨期权还是特定行使价和到期日的看跌期权。波动率表面可以被认为是期权链中所有局部波动率的集合。
什么是波动率期限结构？
波动率期限结构是波动率表面的一部分，它描述了同一股票的期权如何在不同的到期月份表现出不同的隐含波动率，即使对于相同的行使价也是如此。在概念上类似于债券的期限结构（利率根据期限而不同），波动性期限结构可能向上或向下倾斜，具体取决于市场条件和预期。向上倾斜的期限结构表明交易者预计标的股票会随着时间的推移变得更加波动；和一个下降的斜坡，它将变得不那么波动。
总结
波动率面的存在表明Black-Scholes 模型远非准确。但是，市场参与者意识到了这个问题。话虽如此，大多数投资和贸易公司仍然使用布莱克-斯科尔斯模型或它的一些变体。
