波動率面是一個三維圖，顯示了在其上列出的股票期權在不同執行價格和到期日 的隱含波動率。
並非同一股票的所有期權都具有相同的隱含波動率 (IV)。這些差異的存在是由於市場對具有不同特徵的股票期權的定價方式以及股票期權定價模型所說的正確價格應該是多少的差異。
為了更全面地了解這種現象，了解股票期權、股票期權定價和波動率表面的基礎知識非常重要。
關鍵要點
- 波動率表面是指在同一股票上列出的各種期權的隱含波動率的三維圖。
- 隱含波動率用於期權定價，以顯示期權標的股票在期權有效期內的預期波動率。
- Black-Scholes 模型是一種著名的期權定價模型，它在期權定價公式中使用波動率作為其變數之一。
- 波動率表面隨時間變化並且遠非平坦，這表明 Black-Scholes 模型的假設並不總是正確的。
股票期權基礎
股票期權是一種特定類型的衍生證券，賦予所有者執行交易的權利，但沒有義務。在這裡，我們討論一些基本類型的股票期權。
看漲期權
看漲期權賦予所有者在特定日期（稱為到期日）或之前以特定預定價格（稱為行使價（或行使價））購買期權 標的股票的權利。當標的股票價格上漲時，看漲期權的所有者獲利。
看跌期權
看跌期權賦予所有者 在特定日期或之前以特定價格出售期權標的股票的權利。當標的股票價格下跌時，看跌期權的所有者獲利。
其他期權類型
此外，雖然這些名稱與地理無關，但歐式期權只能在到期日執行。相反，美式期權可以在到期日或之前執行。其他類型的期權結構也存在，例如百慕大期權。
期權定價基礎
Black-Scholes 模型是由 Fisher Black、Robert Merton 和 Myron Scholes 在 1973 年開發 的一種期權定價模型，用於對期權定價。1該模型需要六個假設才能起作用：
- 標的股票不支付股息，也永遠不會。
- 該選項必須是歐式的。
- 金融市場是有效的。
- 交易不收取任何傭金。
- 利率保持不變。
- 標的股票收益呈對數正態分布。2
為期權定價的公式稍微複雜一些。它使用以下變數：當前股票價格、距離期權到期的時間、期權的執行價格、無風險利率、股票收益的標準差或波動率。在這些變數之上，該公式使用累積標準正態分布和數學常數「e」，大約為 2.7183。
波動率表面
在 Black-Scholes 模型中使用的所有變數中，唯一不確定的是波動性。在定價時，所有其他變數都是清楚且已知的，但波動性必須是估計值。波動率面是一個三維圖，其中 x 軸是到期時間，z 軸是執行價格，y 軸是隱含波動率。如果 Black-Scholes 模型完全正確，那麼執行價格和到期時間的隱含波動率表面應該是平坦的。在實踐中，情況並非如此。
由於 Black-Scholes 模型的假設並不總是正確的，因此波動率表面遠非平坦，並且經常隨時間變化。例如，行使價較低的期權往往比行使價較高的期權具有更高的隱含波動率。
隨著到期時間接近無限，執行價格的波動趨於收斂到一個恆定水平。然而，經常觀察到波動率表面具有反向波動率微笑。與到期日較長的期權相比，到期時間較短的期權的波動性是其數倍。這種觀察在市場壓力較大的時期更為明顯。應該注意的是，每條期權鏈都是不同的，波動率表面的形狀可能會隨著執行價格和時間而波動。此外，看跌期權和看漲期權通常具有不同的波動率表面。
當您從平價行權價上調或下調行權價時，隱含波動率可能會隨著時間的推移而增加或減少，從而產生一種稱為波動率微笑的形狀，因為它看起來像一個人在微笑。
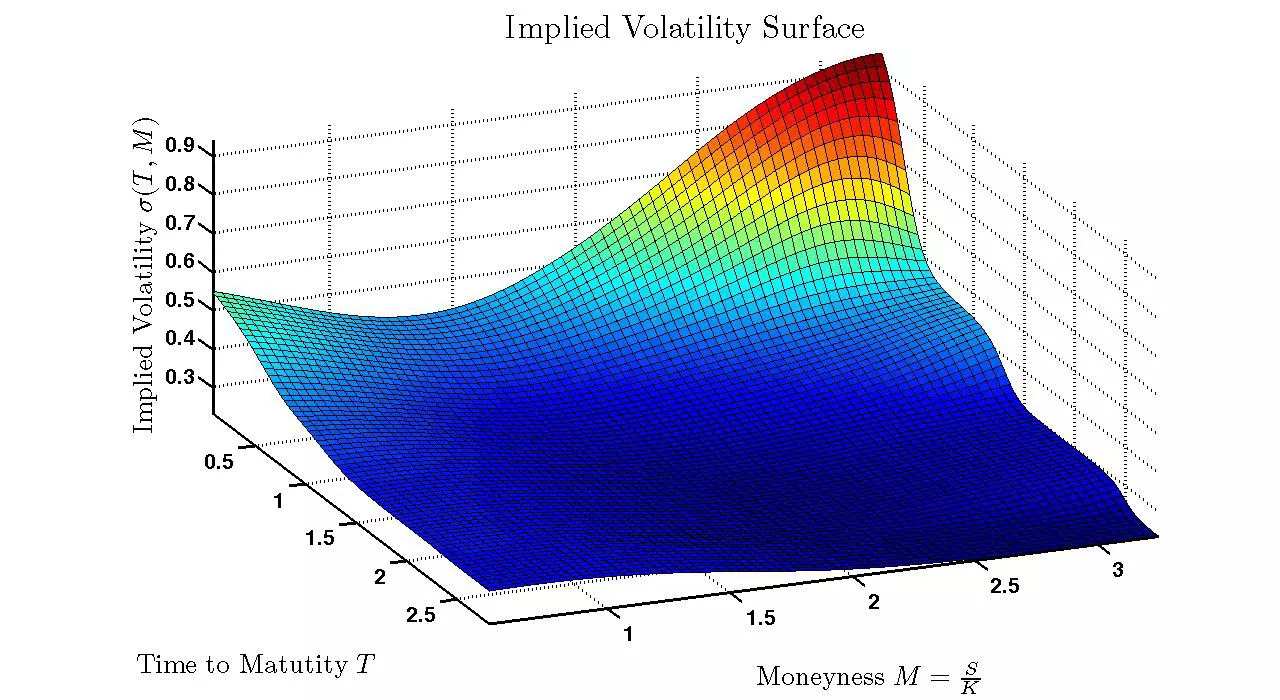波動率表面示例。為什麼會存在波動率偏斜？
自 1980 年代後期以來，期權交易者已經認識到，下行看跌期權在市場中的隱含波動率比他們的模型預測的要高。這是因為天生多頭的投資者和交易者會出於保險目的購買保護性看跌期權。這抬高了看跌期權相對於上行期權的價格。因此，往往存在波動率偏斜。如果上行期權也被買入，有時是由於對潛在收購的預期，那麼就會出現波動率微笑，因為這兩個極端都增加了隱含波動率。
什麼是局部波動率？
局部波動率僅考慮整體波動率表面的一小部分的隱含波動率。它可能只關注一個期權，無論是看漲期權還是特定行使價和到期日的看跌期權。波動率表面可以被認為是期權鏈中所有局部波動率的集合。
什麼是波動率期限結構？
波動率期限結構是波動率表面的一部分，它描述了同一股票的期權如何在不同的到期月份表現出不同的隱含波動率，即使對於相同的行使價也是如此。在概念上類似於債券的期限結構（利率根據期限而不同），波動性期限結構可能向上或向下傾斜，具體取決於市場條件和預期。向上傾斜的期限結構表明交易者預計標的股票會隨著時間的推移變得更加波動；和一個下降的斜坡，它將變得不那麼波動。
總結
波動率面的存在表明Black-Scholes 模型遠非準確。但是，市場參與者意識到了這個問題。話雖如此，大多數投資和貿易公司仍然使用布萊克-斯科爾斯模型或它的一些變體。
