AI 智能摘要
从远古时代开始,当亚当被诱惑苹果去知识之树直到现在,我们可以清楚地发现大自然在我们生活的地球上广告,星星,行星悬浮在我们的视野中,在上面的元素中在我们周围,在每一片草丛中,以及在我们视野中的各种生活形式中,在适当的编号系统中。
你能猜出我在说什么吗?你不必专注于数学来理解这一点。
如果可以的话,为什么不呢?是的,这很简单。我在谈论斐波那契数字。
笑……我知道这对你来说是一个熟悉的术语。到现在为止,你必须明白今天博客的主题是“ 斐波那契和股市分析 ”。
在12 个世纪一个名为莱昂纳多Bonacci意大利数学家谁被认为是“ 中世纪的最有才华的数学家西部 “,写了莱博算盘和普及的印度-阿拉伯数字系统向西方世界。
在唤起你的意识中的任何好奇之前,我想推测一下“Liber Abaci”。
让我引用维基百科“在Liber Abaci(1202)中,斐波那契介绍了所谓的印度语(印第安人的方法),今天称为印度 – 阿拉伯数字。这本书提倡用数字0-9和位置值进行计算。该书通过将数字应用于商业簿记,转换权重和度量,计算利息,货币兑换和其他应用,显示了新阿拉伯数字系统的实际用途和价值。这本书在受过良好教育的欧洲都很受欢迎,对欧洲思想产生了深远的影响。没有已知的1202版本的副本“

你知道斐波那契数列吗?
你必须听到或读到某个基于理想假设的地方,解决了一群涉及兔子生长的问题。
一代又一代地注意到一系列数字,后来被称为斐波纳契数。
要了解有关斐波那契数字的更多信息,你可以完全有权搜索Google。
我们来做一些数学。毕竟,你和我都是交易员。对?
在数学中,这些数字是以下称为斐波纳契数列的整数序列中的数字。
这个序列中有趣的事实是每个数字是前两个数字的总和1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987, 1597,2584,4181,6765,……
 通常通过在该序列的开头添加另一个数字即“0”来修改它。
通常通过在该序列的开头添加另一个数字即“0”来修改它。
我保持简单。
和平。虽然我上面已经提到了Liber Abaci,但更确切地说,我想提一下,这个序列早先在印度数学中被描述为Virahanka数字。
这些数字与黄金比例密切相关。我稍后会解释。
起源
根据维基百科“ Fibonacci序列出现在印度数学中,与梵语韵律有关。
在梵文的韵律传统中,人们有兴趣列举2个单位持续时间的长(L)音节的所有模式,以及1个持续时间单位的短(S)音节。
计算给定持续时间的L和S的不同模式导致斐波那契数:m个短音节长的模式的数量是斐波纳契数F m + 1。
Susantha Goonatilake写道,Fibonacci序列的发展“部分归因于Pingala(公元前200年),后来与Virahanka(公元700年),Gopāla(约1135年)和Hemachandra(约1150年)有关。”
Parmanand Singh引用Pingala的神秘公式(“两者混合”)并引用在上下文中解释它的学者说 m 节拍(F m + 1)的情况是通过添加 [ S]到F m的 情况和[L]到F m -1的 情况。他在公元前450年前与Pingala约会。
然而,序列的最清晰的阐述出现在Virahanka(公元700年)的工作中,其自己的工作已经丢失,但可以在Gopala的引文中 找到(c.1135 )。
“ 斐波那契序列 ” 这个名字最初是由19世纪的数字理论家爱德华·卢卡斯使用的。
黄金比例
我听说你在嘀咕着这个公式。
是的,这很简单。
如果它们的比率与它们的总和与两个量中较大的一个的比率相同,则称任何两个量为黄金比例或黄金分割或黄金分割。
让我简化一下。
下图说明了几何关系。
假设a和b是可量化的,其中a> b> 0,因此我们得到
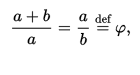
希腊字母phi代表黄金比例。
它的价值在于
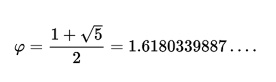
它有很多绰号。这个比例本质上是出现在一些模式中。
金色矩形
它是一个矩形,其长度和宽度是黄金比例,其中phi约为1.618。
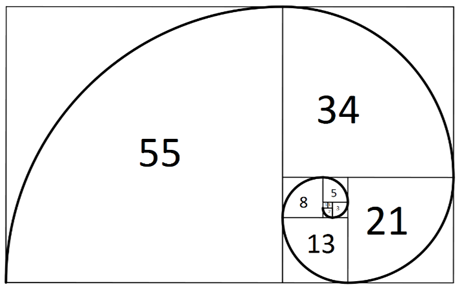
金色螺旋
它从一个矩形开始,其长度和宽度之比是黄金比例。
令人惊讶的是,这个矩形可以被分割成正方形和类似的矩形,并且该过程可以继续。
在按照你喜欢或尽可能多的时间继续该过程之后,最终结果将是矩形几乎完全分成正方形。
然后你可以用四分之一圆圈连接这些方块的角。
虽然它不会是一个完美的对数螺旋,但相信我它会接近一个金色螺旋。
斐波那契比率本质上
你知道斐波纳契数是自然界不可或缺的一部分。
根据这个星球上一些最好的大脑,你可以在以太及其时尚的星光熠熠的家庭中找到它。
撇开较大的部分让我们专注于Akash Ganga的第三个星球。
我惊讶地发现,从植物的叶子排列到花朵的小花图案,一粒小麦到一个智人的单细胞,这些数字编织了整个自然界的一定数量的数字。不是很有趣吗?
让我分享更多的事实。你见过葵花了吗?
?如果没有,那么去你的邻居花园,你一定会找到一个。
你知道它包含Fibonacci系列的数字吗?是的,有时89或144。

此外,它有一个金色的螺旋种子安排。
海星有五条臂,你必须知道这是一个斐波那契数。
我再给你一个例子。你知道有鹦鹉螺的外壳有金色的比例。这是一个对数螺旋。很有魅力,不是吗?你可以使用Google找到更多内容。
斐波那契序列中的一些基本概念:
- 如果你将数字除以前一个数字,你将获得1.618
示例=> 377/233 = 1.618
- 数字除以下面的数字将给出0.618.这是61.8%回撤的基础。让我读一下你的想法。你必须考虑“回撤”一词。对?我稍后会解释你。你继续抢劫基本概念。
示例=> 144/233 = 0.618
- 我想告诉你一些事情。让我再次写序列1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,…
144/233 = 0.618; 89/144 = 0.618; 55/89 = 0.618
144/377 = 0.382
89/377 = 0.236
0.382 / 0.618 = 0.618
0.236 / 0.382 = 0.618
377/233 = 1.618
377/144 = 2.618
377/89 = 4.236
1.618 / 2.618 = 0.618
2.618 / 4.236 = 0.618
你一定爱上了这种永恒的分析技术。
作为交易者,这是显而易见的。
无论时间框架和市场条件如何,它在确定进入和止损水平方面都发挥着重要作用。
如果你不使用此工具,请开始使用它。
我们是情感的生物,生物充满了偏见,并受到骄傲和虚荣的激励。在华尔街有一句老话说, 市场只受两种情绪驱动,即贪婪和恐惧。
因此,在没有判断交易者和投资者进入市场的适当价格水平的情况下,也没有适当的保护,即止损水平。
一个愚蠢的错误可能会破坏可能有利可图的结果,当且仅当他或她在准确的价格水平下有适当的目标时。
如果你认为在下次交易中你将使用这个简单的工具,我感谢你的思考过程。它走在正确的轨道上。
在外行人的术语中,它可以用于识别或确认关键的需求和供应水平,即支撑和阻力水平。
此外,它还有助于确定价格目标。
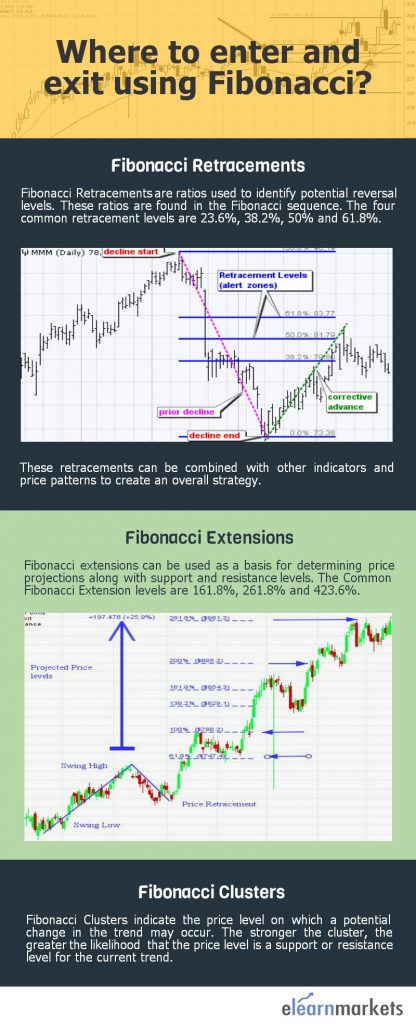
斐波纳契回撤
由于你已经熟悉斐波那契,现在让我们专注于斐波纳契回撤。
它专门用于确定支撑和阻力水平。
它基于这样一种观点,即市场将追溯可预测的一部分。
在此之后,它将继续沿着原来的方向前进。
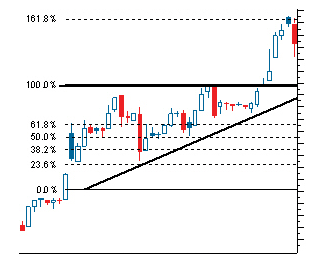
根据维基百科“ 斐波那契回撤是通过在图表上取两个极值点并将垂直距离除以关键的斐波那契比率来创建的。
0.0%被认为是回撤的开始,而100.0%完全逆转了原始部分。
确定这些水平后,绘制水平线并用于识别可能的支撑和阻力水平“。
绘制起来非常简单。
只需画出高低之间的趋势线,然后将垂直距离除以关键的斐波纳契比率23.6%,38.2%,50%,61.8%和100%。
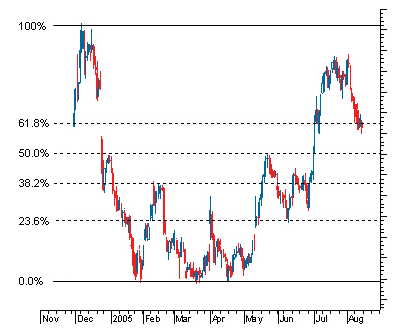
资料来源:Investopedia
斐波那契扩展
这些都很简单。
根据investopedia “它用于斐波那契回撤来预测市场的阻力和支撑空间。这些扩展涉及超过基本100%级别的所有级别。
交易者经常使用它来确定将带来利润的所谓空间“。
扩展水平主要为61.8%,100%,138.2%,161.8%,200%,238.2%,261.8%。
请记住以下两点
- 斐波那契在上升
在摆动方向对面画出斐波那契。
因此,在上升时从最后一个顶部到最后一个底部(始终从左到右)绘制它。
如果水平高于高位,则标记161.8%,261.8%和423.6%,如果低于,则可以自由忽略它们。
- 下滑的斐波那契
在摆动方向对面画出斐波那契。
所以,在下滑时将它从最后一个底部拉到最后一个顶部(总是从左到右)。
如果水平低于低,则标记161.8%,261.8%和423.6%,如果高于,则可以忽略它们。
总结
相信我可以添加很多东西。
但它超出了本文的范围。
有一个共同的格言“冠军继续比赛,直到他们做对了”。
因此,像削尖斧头一样,尽量使用此工具来提高你的交易并最大化利润。
总是很好“ 首先计划你的交易,然后交易你的计划 ”。