AI 智能摘要
定义: 最小方差投资组合表示一个多元化的投资组合,由单独的风险资产组成,这些资产在交易时进行对冲,从而使预期回报率的风险最小。
最小方差投资组合意味着什么?
最小方差组合的定义是什么? 这可以利用 抵消投资来利用每个单独资产的 风险,从而针对预期的投资组合回报率对冲所接受风险水平的总投资组合风险 。
简单地说,如果单独交易,每个投资在最小差异投资组合中都是有风险的,但是当在投资组合中交易时,风险就会被对冲。该术语源于Markowitz投资组合理论,该理论表明波动率可用于替代风险,因此波动率差异较小与投资风险较小相关。
我们来看一个例子。
例
安德鲁是一名金融分析师,他在一家咨询公司工作。他的经理要求安德鲁计算该公司最杰出客户持有的几个风险股票的最小差异投资组合。
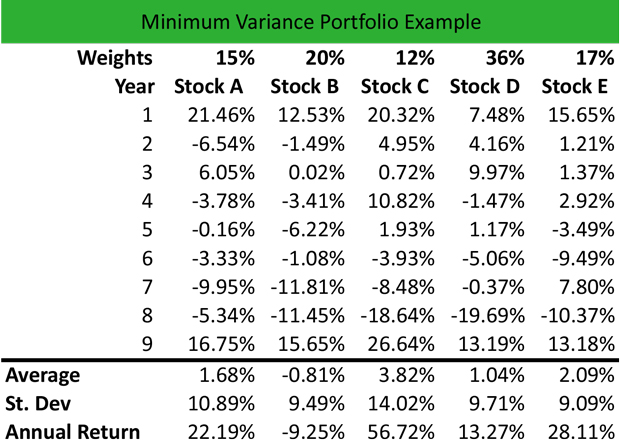
投资组合投资五只股票,分配比例分别为15%,20%,12%,36%和17%。Andrew使用Excel中的STDEV函数计算标准差,并使用平均回报计算每个股票的年度回报,如下所示:
年度回报股票A =(1+平均回报)t-1 =(1 + 1.68%)12-1 = 22.19%等等剩余股票。
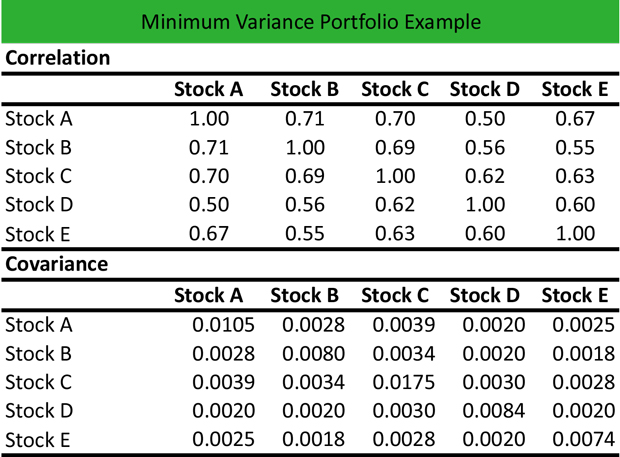
然后,Alex计算投资组合中包含的股票的相关性和协方差,以构建可以最小化风险的优化投资组合。他在Excel中应用相关矩阵来调查股票收益之间的相关性,并使用Excel中的VARP函数计算协方差,以查找每个股票的收益平均值,如下所示:
然后,他使用每个股票的权重和协方差来构建优化的投资组合。权重总和等于1(100%)。
优化推导如下:
- 库存A:0.15×0.0105×0.15 = 0.0002
- 库存B:0.20×0.0028×0.20 = 0.0001
- 库存C:0.12×0.0039×0.12 = 0.0001
- 库存D:0.36×0.0020×0.36 = 0.0001
- 库存E:0.17×0.0025×0.17 = 0.0001
相同的公式适用于每个权重,从而得出每个股票的总优化回报,如下所示:
安德鲁通过添加每个股票的个别价值来计算投资组合差异:
投资组合差异= 0.0006 + 0.0007 + 0.0006 + 0.0016 + 0.0005 = 0.0040 = 0.40%
然后,他计算投资组合标准差:
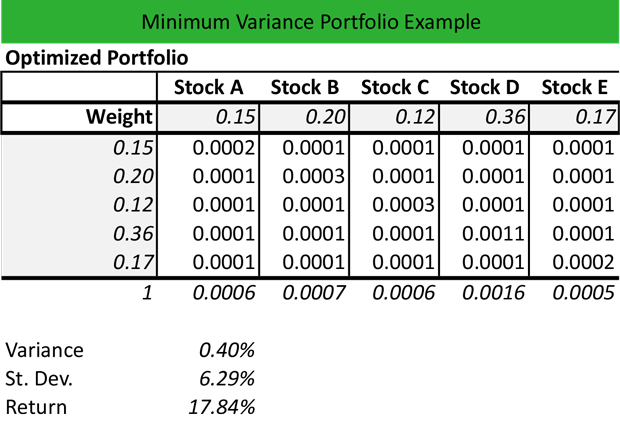
投资组合标准差=投资组合差异0.5 = 0.00400.5 = 0.0629 = 6.29%
最后,他使用每个股票的权重乘以股票的年度回报来计算优化的投资组合回报,如下所示:
优化投资组合收益率= 0.15 x 22.19%+ 0.20 x(-9.25%)+ 0.12 x 56.72%+ 0.36 x 13.27%+ .017 x 28.11%= 3.33%-1.85%+ 6.81%+ 4.78%+ 4.78%= 17.84%
摘要定义
定义最小方差投资组合: MVP意味着一个多元化的投资组合,可以恰当地降低风险。
