尾部風險是投資組合風險的一種形式，當一項投資偏離均值超過三個標準差的可能性大於正態分布所顯示的值時，就會出現這種風險。
尾部風險包括發生概率較小且發生在正態分布曲線兩端的事件。
關鍵要點
- 尾部風險是由概率分布預測的由於罕見事件而發生損失的可能性。
- 通俗地說，超過三個標準差的短期移動被認為是尾部風險的實例化。
- 雖然尾部風險在技術上指的是左右尾，但人們最關心的是損失（左尾）。
- 尾部事件讓專家質疑可投資資產回報的真實概率分布。
了解尾部風險
傳統的投資組合策略通常遵循市場回報服從正態分布的想法。然而，尾部風險的概念表明，收益的分布不是正態的，而是偏斜的，並且有更肥的尾巴。
肥尾表明，投資有可能超過三個標準差 ，這可能比預期的要大。例如，在查看對沖基金回報 時，經常會看到以肥尾為特徵的分布。
下圖描繪了三個向右偏斜增加的曲線，肥尾向下，與正態分布 的對稱鐘形曲線形狀不同。
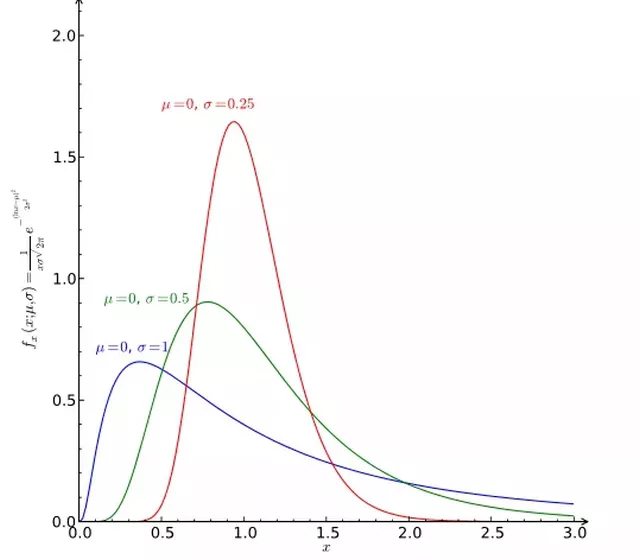右偏度。正態分布和資產回報
當投資組合放在一起時，假設收益分布將遵循正態分布。在此假設下，收益在均值和三個標準差（正或負）之間變動的概率約為 99.7%。這意味著收益超出均值超過三個標準差的概率為 0.3%。
市場收益服從正態分布的假設是許多金融模型的關鍵，例如 Harry Markowitz 的現代投資組合理論 (MPT)和 Black-Scholes-Merton期權定價模型。然而，這種假設並不能正確反映市場收益，尾部事件對市場收益的影響很大。
Nassim Taleb 的暢銷金融書籍《黑天鵝》中強調了尾部風險。
其他分布及其尾巴
股票市場回報傾向於遵循具有過度峰度的正態分布。峰度是一種統計量度，表明觀察到的數據是否遵循與正態分布相關的重尾分布或輕尾分布。正態分布曲線的峰度等於 3，因此，如果證券遵循峰度大於 3 的分布，則稱其為肥尾。
尖峰分布，或重/肥 尾分布，描述了極端結果發生得比預期多的情況。與正態分布相比，這些曲線具有過多的峰度。因此，遵循這種分布的證券所經歷的回報超過了平均值的三個標準差，超過了觀察結果的 0.3%。
下圖描繪了正態分布（綠色）以及越來越多的尖峰曲線（紅色和藍色），它們顯示出肥尾。
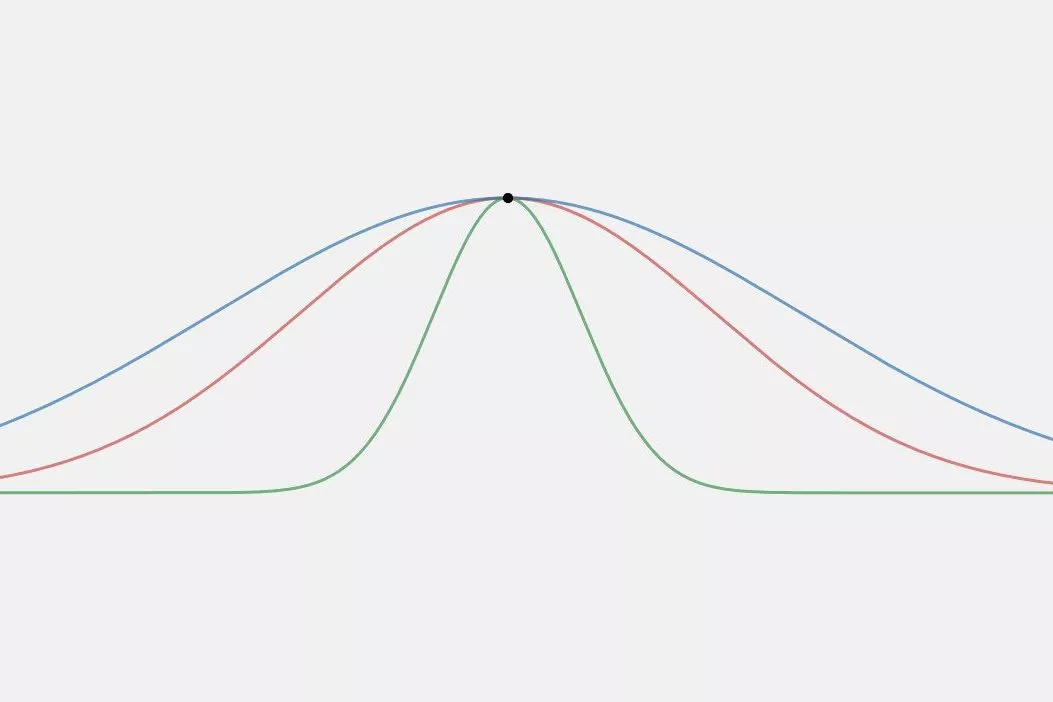峰度描述了概率分布可能具有的不同類型的峰值。
思想公司
對沖尾部風險
儘管對投資組合產生負面影響的尾部事件很少見，但它們可能會產生很大的負回報。因此，投資者應對沖這些事件。對沖尾部風險旨在提高長期回報，但投資者必須承擔短期成本。投資者可能希望分散他們的投資組合以對沖尾部風險。
例如，如果投資者是跟蹤標準普爾 500 指數 (S&P 500) 的多頭交易所交易基金 (ETF) ，則投資者可以通過購買與 Cboe 波動率指數成反比的衍生品來對沖尾部風險。標準普爾 500 指數。
