AI 智能摘要
资本资产定价模型 (CAPM) 描述了系统性风险或投资的一般风险与资产(尤其是股票)的预期回报之间的关系。1CAPM 演变为一种衡量这种系统性风险的方法。考虑到这些资产的风险和资本成本,它在整个金融领域被广泛用于对风险证券进行定价并为资产产生预期回报。
资本资产定价模型 – CAPM
了解资本资产定价模型 (CAPM)
给定风险的资产的预期收益计算公式如下:1
\begin{aligned} &ER_i = R_f + \beta_i (ER_m – R_f) \\ &\textbf{其中:} \\ &ER_i = \text{预期投资回报} \\ &R_f = \text{无风险利率} \ \ &\beta_i = \text{投资的beta} \\ &(ER_m – R_f) = \text{市场风险溢价} \\ \end{对齐}ER _一世=RF+b一世( E R米−RF)在哪里:ER _一世=预期投资回报RF=无风险利率b一世=投资的贝塔( E R米−RF)=市场风险溢价
投资者期望得到补偿的风险和货币的时间价值。CAPM 公式中的无风险利率说明了货币的时间价值。CAPM 公式的其他组成部分说明了投资者承担的额外风险。
潜在投资的贝塔是衡量该投资会给看起来像市场的投资组合增加多少风险的指标。如果一只股票比市场风险更大,它的贝塔系数就会大于 1。如果一只股票的贝塔系数小于 1,则该公式假定它将降低投资组合的风险。
然后将股票的贝塔乘以市场风险溢价,即市场预期的高于无风险利率的回报。然后将无风险利率加到股票的贝塔和市场风险溢价的乘积上。结果应该为投资者提供他们可以用来找到资产价值 的所需回报或贴现率。
CAPM 公式的目标是评估当股票的风险和货币时间价值与其预期收益进行比较时,它的估值是否公允。换句话说,通过了解 CAPM 的各个部分,可以判断股票的当前价格是否与其可能的回报一致。
例如,假设一位投资者正在考虑今天每股价值 100 美元的股票,该股票每年支付 3% 的股息。与市场相比,该股票的贝塔系数为 1.3,这意味着它比市场投资组合风险更大。此外,假设无风险利率为 3%,该投资者预计市场价值每年上涨 8%。
基于 CAPM 公式的股票预期回报率为 9.5%:
\begin{aligned} &9.5\% = 3\% + 1.3 \times ( 8\% – 3\% ) \\ \end{aligned}9.5%=3%+1.3×(8%−3%)
CAPM 公式的预期收益用于折现股票在预期持有期间的预期股息和资本增值。如果这些未来现金流的贴现值等于 100 美元,那么 CAPM 公式表明股票相对于风险的估值是公允的。
CAPM 的问题
CAPM 公式背后的几个假设已被证明在现实中不成立。现代金融理论基于两个假设:第一,证券市场非常有竞争力和效率(即,有关公司的相关信息可以迅速、普遍地分布和吸收);第二,这些市场由理性的、规避风险的投资者主导,他们寻求最大程度地满足他们的投资回报。
因此,CAPM 是否有效尚不完全清楚。最大的症结在于测试版。当 Eugene Fama 和 Kenneth French 教授研究纽约证券交易所、美国证券交易所和纳斯达克的股票回报时,他们发现长期贝塔的差异并不能解释不同股票的表现。贝塔系数和个股回报率之间的线性关系也会在较短的时间内分解。这些发现似乎表明 CAPM 可能是错误的。2
尽管存在这些问题,但 CAPM 公式仍然被广泛使用,因为它简单并且可以轻松比较投资选择。
在公式中包含贝塔假设风险可以通过股票的价格波动来衡量。然而,两个方向的价格变动风险并不相同。确定股票波动率的回溯期不是标准的,因为股票收益(和风险)不是正态分布的。
CAPM 还假设无风险利率在贴现期内保持不变。假设在前面的例子中,美国国债的利率在 10 年的持有期内上升到 5% 或 6%。无风险利率的提高也会增加投资所用资金的成本,并可能使股票看起来被高估。
用于寻找市场风险溢价的市场组合只是一个理论值,而不是可以作为股票的替代品购买或投资的资产。大多数时候,投资者会使用标准普尔500等主要股票指数来替代市场,这是一个不完美的比较。
对 CAPM 最严重的批评是假设可以为贴现过程估计未来现金流量。如果投资者可以高度准确地估计股票的未来回报,则不需要 CAPM。
CAPM 和有效前沿
使用 CAPM 建立投资组合应该可以帮助投资者管理风险。如果投资者能够使用 CAPM 来完美优化投资组合相对于风险的回报,它将存在于一条称为有效前沿的曲线上,如下图所示。
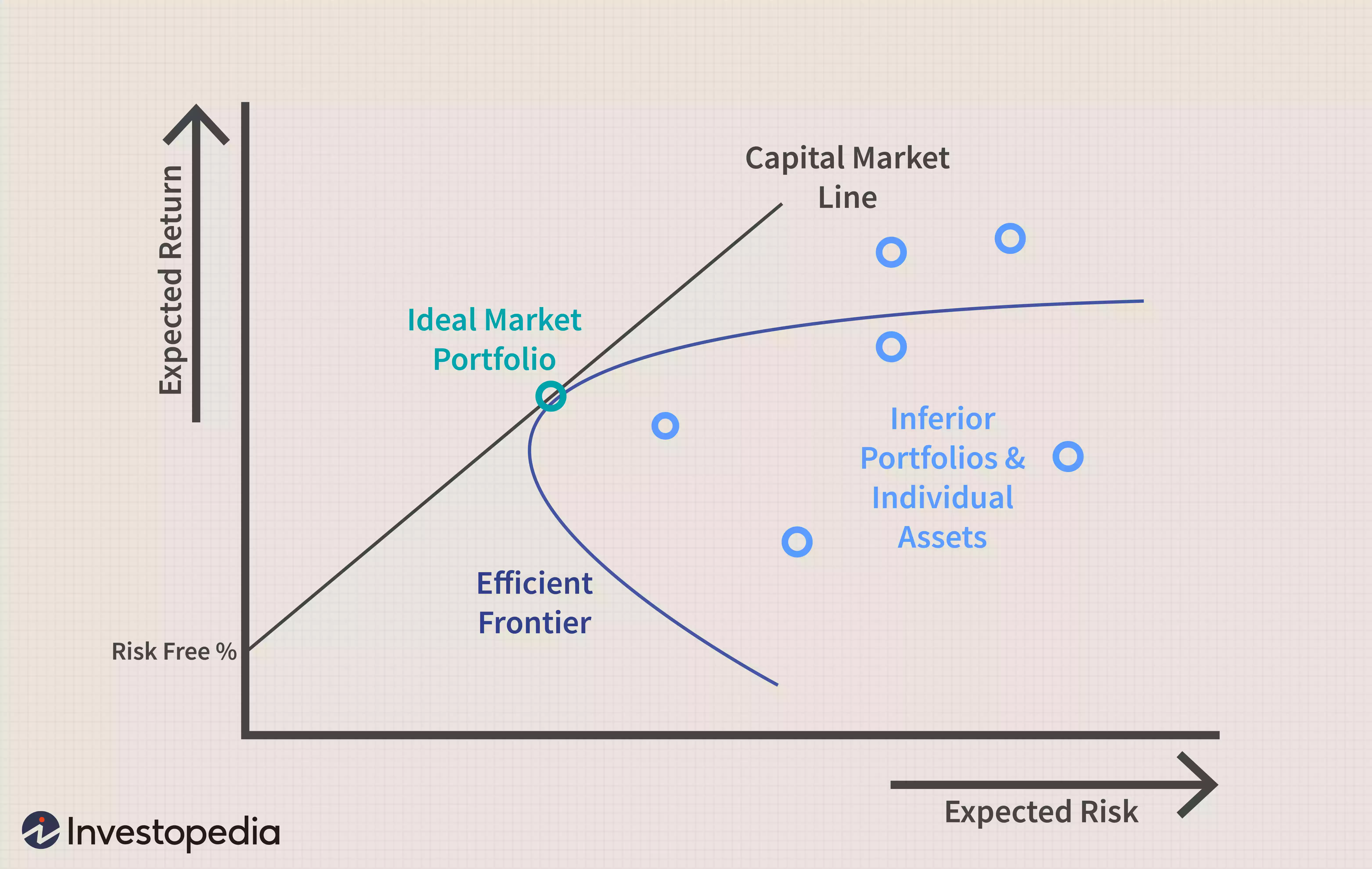
图片由 Julie Bang © Investopedia 2022
该图显示了更大的预期回报(y 轴)如何需要更大的预期风险(x 轴)。现代投资组合理论 (MPT)表明,从无风险利率开始,投资组合的预期收益随着风险的增加而增加。任何适合资本市场线 (CML)的投资组合都比该线右侧的任何可能的投资组合要好,但在某些时候,可以在 CML 上构建理论投资组合,并在所承担的风险量下获得最佳回报.
CML 和有效边界可能难以定义,但它们向投资者说明了一个重要概念:增加回报和增加风险之间存在权衡。由于不可能完美地构建适合 CML 的投资组合,因此投资者在寻求额外回报时承担过多风险更为常见。
在下图中,您可以看到两个已构建以适应有效边界的投资组合。投资组合 A 预计每年的回报率为 8%,标准差或风险水平为 10%。投资组合 B 预计每年的回报率为 10%,但标准差为 16%。投资组合 B 的风险上升速度快于预期回报。
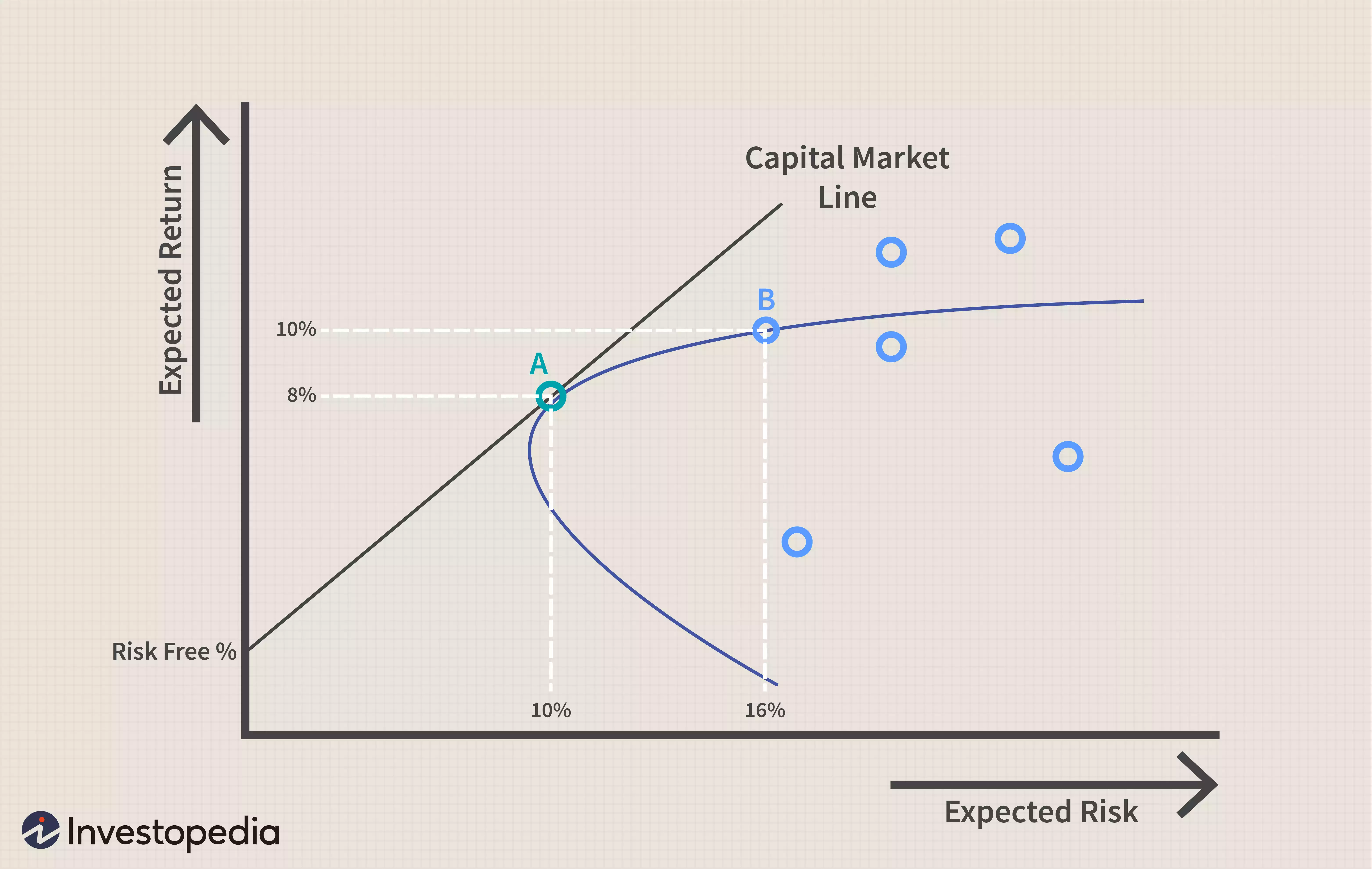
图片由 Julie Bang © Investopedia 2022
有效边界假设与 CAPM 相同,只能在理论上计算。如果投资组合存在于有效边界上,它将为其风险水平提供最大回报。但是,不可能知道投资组合是否存在于有效前沿,因为无法预测未来收益。
这种风险和回报之间的权衡适用于 CAPM,并且可以重新排列有效边界图以说明单个资产的权衡。在下图中,您可以看到 CML 现在称为证券市场线 (SML)。而不是 x 轴上的预期风险,而是使用股票的贝塔值。正如您在插图中看到的,随着 beta 从 1 增加到 2,预期回报也在上升。
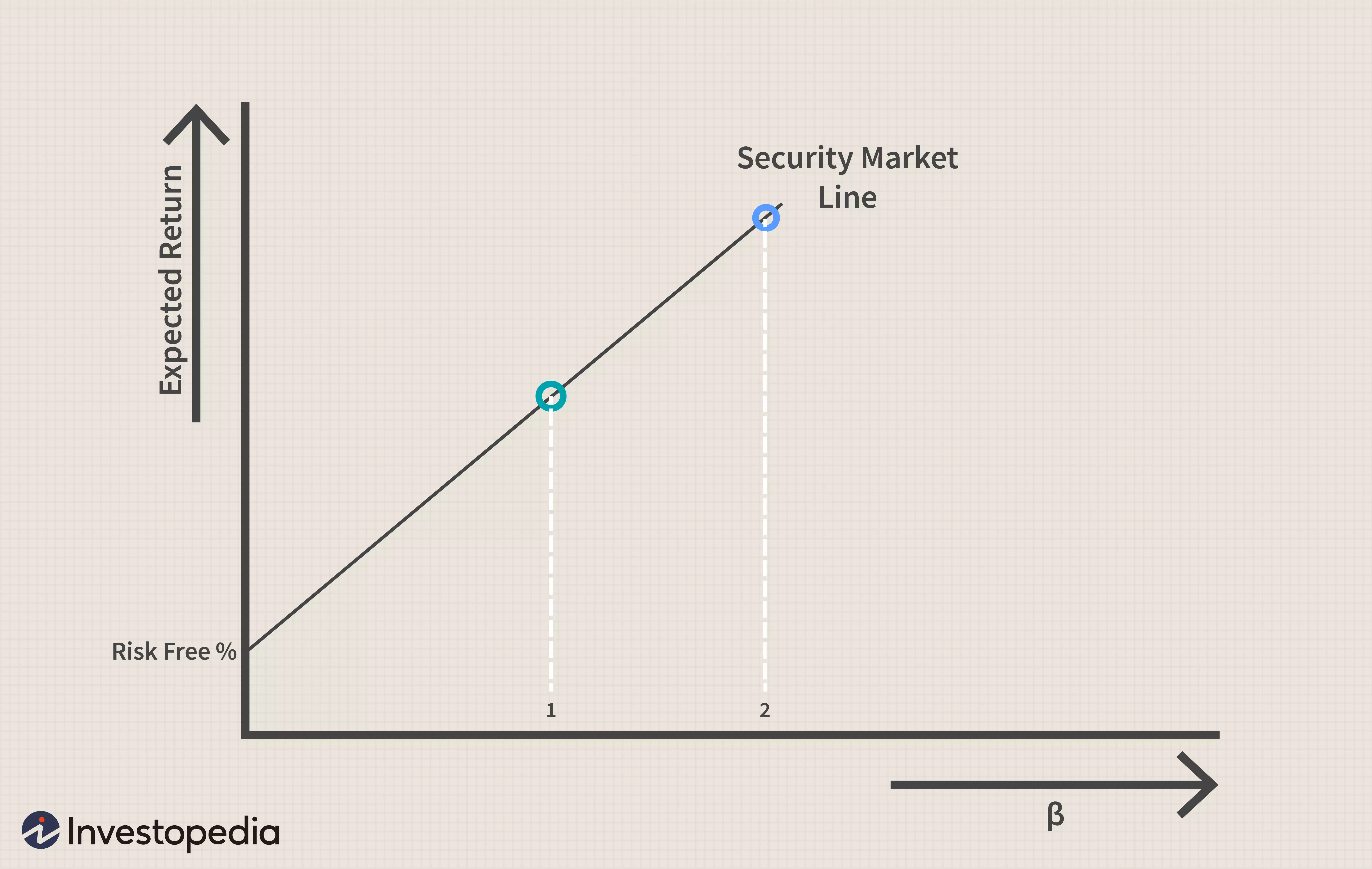
图片由 Julie Bang © Investopedia 2022
CAPM 和 SML 将股票的贝塔系数与其预期风险联系起来。Beta 是通过对单个每日股价回报与市场在同一时期的每日回报进行比较的统计分析得出的。更高的贝塔意味着更多的风险,但高贝塔股票组合可能存在于 CML 上的某个地方,即使不是理论上的理想,也可以接受权衡。
这两个模型的价值被关于贝塔和市场参与者的假设削弱了,这些假设在真实市场中是不真实的。例如,与另一只具有相同高贝塔但没有经历相同类型的价格下跌的股票相比,贝塔值并不能说明比市场波动更大、下行冲击频率高的股票的相对风险。 .
CAPM的实用价值
考虑到对 CAPM 的批评以及其在投资组合构建中使用背后的假设,可能很难看出它有什么用处。但是,使用 CAPM 作为评估未来预期合理性或进行比较的工具仍然具有一定的价值。
想象一下,一位顾问建议以 100 美元的股价将一只股票添加到投资组合中。顾问使用 CAPM 以 13% 的折扣率证明价格合理。顾问的投资经理可以获取这些信息并将其与公司过去的业绩和同行进行比较,看看 13% 的回报是否是一个合理的预期。
假设在这个例子中,同行集团在过去几年的表现略好于 10%,而这只股票一直表现不佳,回报率为 9%。投资经理不应在没有为增加的预期回报提供理由的情况下接受顾问的建议。
投资者还可以使用 CAPM 和有效前沿的概念来评估他们的投资组合或个股与市场其他部分的表现。例如,假设投资者的投资组合在过去三年中每年的回报率为 10%,回报率(风险)的标准差为 10%。然而,过去三年市场平均回报率为 10%,风险为 8%。
投资者可以利用这一观察结果重新评估他们的投资组合是如何构建的,以及哪些资产可能不在 SML 上。这可以解释为什么投资者的投资组合在 CML 的右侧。如果可以识别出拖累回报或不成比例地增加投资组合风险的持股,投资者可以做出改变以提高回报。毫不奇怪,CAPM 促进了规避风险的投资者使用指数或组合股票组合以模仿特定市场或资产类别的增加。这主要是由于 CAPM 的信息,即只有通过承担更高的风险(beta)才能获得比整个市场更高的回报。
总结
CAPM 使用现代投资组合理论的原则来确定证券是否被公允估值。它依赖于与现实不符的投资者行为、风险和回报分布以及市场基本面的假设。然而,CAPM 的基本概念和相关的有效边界可以帮助投资者理解预期风险和回报之间的关系,因为他们努力做出关于将证券添加到投资组合的更好决策。


